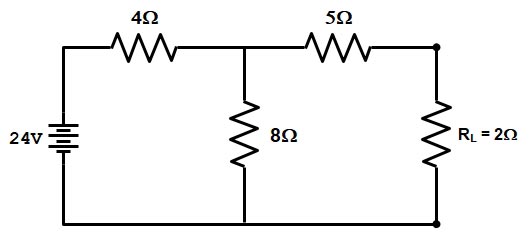
As per Thevenin theorem, when resistance RL is connected across terminals A and B, the network behaves as a source of voltage ETh and internal resistance RT and this is called Thevenin equivalent circuit.
Thevenin Voltage
The Thevenin voltage used in Thevenin’s Theorem is an ideal voltage source equal to the open circuit voltage at the terminals.
In the given question, the resistance 10Ω does not affect this voltage and the resistances 30Ω and 20Ω form a voltage divider, giving
\begin{array}{l}{E_{Th}} = 100 \times \dfrac{30}{{30 + 20}}\\\\{E_{TH}} = 60V\end{array}
Thevenin’s resistance can be found by replacing 100 V source with a short-circuit.
Thevenin equivalent resistance for the given network is
R = (R1 || R2) + R3
Rth = (20 || 30) + 10 = (20 x 30) ⁄ (20 + 30) + 10 = 22Ω
Rth = 22Ω
The Load current Is calculated as
IL = ETH ⁄ (RTH + RL)
= 60 ⁄ (22 + 5) = 2.22 A
Hence the value of Thevenin voltage, Thevenin Resistance, and Load current is (60 V, 22Ω, 2.22A) respectively.