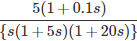A control system has open loop transfer function . Break away point is lies between
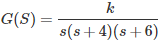
YOUR ANSWER : ?
 EXAMIANS
EXAMIANS